7. Indexing and transposing a table¶

In this lecture we demonstrate:

how indexing a table provides flexible access to the elements of the table;
how to compute accross rows and columns of the table; and
how to transpose a table.

7.1. Indexing¶

We have seen that working with columns of a DataFrame is very easy because colums have names. It would be as easy to work with rows of a DataFrame if we had a way to name the rows somehow. The process that does precisely that is called the indexing of a table.

To index a table we first have to identify a column (the indexing column or the index) such that each row in uniquely determined by the value in the indexing column. For example, in the following table

Name	Sex	Age (yrs)	Weight (kg)	Height (cm)
Anne	f	13	46	160
Ben	m	14	52	165
Colin	m	13	47	157
Diana	f	15	54	165
Ethan	m	15	56	163
Fred	m	13	45	159
Gloria	f	14	49	161
Hellen	f	15	52	164
Ian	m	15	57	167
Jane	f	13	45	158
Kate	f	14	51	162

"Name" is a good candidate for the indexing column because in this table vevery student has a unique name (note that in real life this is not necessarily the case). "Height" is not a good choice because there are two students whose height is 165; and the same goes for other columns.

The function set_index sets the index column of the table:

In [1]:

import pandas as pd
students = [["Anne",    "f", 13, 46, 160],
            ["Ben",     "m", 14, 52, 165],
            ["Colin",   "m", 13, 47, 157],
            ["Diana",   "f", 15, 54, 165],
            ["Ethan",   "m", 15, 56, 163],
            ["Fred",    "m", 13, 45, 159],
            ["Gloria",  "f", 14, 49, 161],
            ["Hellen",  "f", 15, 52, 164],
            ["Ian",     "m", 15, 57, 167],
            ["Jane",    "f", 13, 45, 158],
            ["Kate",    "f", 14, 51, 162]]
students_df = pd.DataFrame(students)
students_df.columns=["Name", "Sex", "Age", "Weight", "Height"]

students_ix=students_df.set_index("Name")

The new table (students_ix) differs from the old one (students_df) only in the fact that the rows of the table are now indexed by the names of the students. Here is the unidexed version of the table:

In [2]:

students_df

Out[2]:

	Name	Sex	Age	Weight	Height
0	Anne	f	13	46	160
1	Ben	m	14	52	165
2	Colin	m	13	47	157
3	Diana	f	15	54	165
4	Ethan	m	15	56	163
5	Fred	m	13	45	159
6	Gloria	f	14	49	161
7	Hellen	f	15	52	164
8	Ian	m	15	57	167
9	Jane	f	13	45	158
10	Kate	f	14	51	162

and here is the indexed version of the same table:

In [3]:

students_ix

Out[3]:

	Sex	Age	Weight	Height
Name
Anne	f	13	46	160
Ben	m	14	52	165
Colin	m	13	47	157
Diana	f	15	54	165
Ethan	m	15	56	163
Fred	m	13	45	159
Gloria	f	14	49	161
Hellen	f	15	52	164
Ian	m	15	57	167
Jane	f	13	45	158
Kate	f	14	51	162

The column "Name" is still present, but now it has a special statis. If we try to access it as we did before we get an error (the error report is quite long; don't bother reading it carefully, just scroll down):

In [4]:

students_ix["Name"]

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\indexes\base.py in get_loc(self, key, method, tolerance)
   3077             try:
-> 3078                 return self._engine.get_loc(key)
   3079             except KeyError:

pandas\_libs\index.pyx in pandas._libs.index.IndexEngine.get_loc()

pandas\_libs\index.pyx in pandas._libs.index.IndexEngine.get_loc()

pandas\_libs\hashtable_class_helper.pxi in pandas._libs.hashtable.PyObjectHashTable.get_item()

pandas\_libs\hashtable_class_helper.pxi in pandas._libs.hashtable.PyObjectHashTable.get_item()

KeyError: 'Name'

During handling of the above exception, another exception occurred:

KeyError                                  Traceback (most recent call last)
<ipython-input-4-475864f81b1d> in <module>
----> 1 students_ix["Name"]

C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\frame.py in __getitem__(self, key)
   2686             return self._getitem_multilevel(key)
   2687         else:
-> 2688             return self._getitem_column(key)
   2689 
   2690     def _getitem_column(self, key):

C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\frame.py in _getitem_column(self, key)
   2693         # get column
   2694         if self.columns.is_unique:
-> 2695             return self._get_item_cache(key)
   2696 
   2697         # duplicate columns & possible reduce dimensionality

C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\generic.py in _get_item_cache(self, item)
   2487         res = cache.get(item)
   2488         if res is None:
-> 2489             values = self._data.get(item)
   2490             res = self._box_item_values(item, values)
   2491             cache[item] = res

C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\internals.py in get(self, item, fastpath)
   4113 
   4114             if not isna(item):
-> 4115                 loc = self.items.get_loc(item)
   4116             else:
   4117                 indexer = np.arange(len(self.items))[isna(self.items)]

C:\ProgramData\Anaconda3\lib\site-packages\pandas\core\indexes\base.py in get_loc(self, key, method, tolerance)
   3078                 return self._engine.get_loc(key)
   3079             except KeyError:
-> 3080                 return self._engine.get_loc(self._maybe_cast_indexer(key))
   3081 
   3082         indexer = self.get_indexer([key], method=method, tolerance=tolerance)

pandas\_libs\index.pyx in pandas._libs.index.IndexEngine.get_loc()

pandas\_libs\index.pyx in pandas._libs.index.IndexEngine.get_loc()

pandas\_libs\hashtable_class_helper.pxi in pandas._libs.hashtable.PyObjectHashTable.get_item()

pandas\_libs\hashtable_class_helper.pxi in pandas._libs.hashtable.PyObjectHashTable.get_item()

KeyError: 'Name'

However, it is there as an index column:

In [5]:

students_ix.index

Out[5]:

Index(['Anne', 'Ben', 'Colin', 'Diana', 'Ethan', 'Fred', 'Gloria', 'Hellen',
       'Ian', 'Jane', 'Kate'],
      dtype='object', name='Name')

Visualizing, say, the height of the students in the group now works like this:

In [6]:

import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.bar(students_ix.index, students_ix["Height"])
plt.title("The height of students")
plt.show()
plt.close()

<Figure size 1000x500 with 1 Axes>

7.2. Accessing rows and individual cells of an indexed table¶

DataFrame is optimized to provide efficient access to the columns of the table. However, in an indexed DataFrame it is also easy to access rows and cells of the table using the function loc (short for "location").

We can display a single row of the table like this:

In [7]:

students_ix.loc["Ethan"]

Out[7]:

Sex         m
Age        15
Weight     56
Height    163
Name: Ethan, dtype: object

or a range of rows like this:

In [8]:

students_ix.loc["Ethan":"Ian"]

Out[8]:

	Sex	Age	Weight	Height
Name
Ethan	m	15	56	163
Fred	m	13	45	159
Gloria	f	14	49	161
Hellen	f	15	52	164
Ian	m	15	57	167

We can also focus on a particular feature:

In [9]:

students_ix.loc["Ethan", "Height"]

Out[9]:

or display a set of features for a set of rows:

In [10]:

students_ix.loc["Ethan":"Ian", "Weight":"Height"]

Out[10]:

	Weight	Height
Name
Ethan	56	163
Fred	45	159
Gloria	49	161
Hellen	52	164
Ian	57	167

7.3. Computing accross rows and columns of an indexed table¶

In the table below we have collected the marks of students we have already met in some subjects (Computers, English, Maths, Physics, Chemistry and Arts):

In [11]:

marks = [["Anne",    5, 3, 5, 2, 4, 5],
         ["Ben",     5, 5, 5, 5, 5, 5],
         ["Colin",   4, 5, 3, 4, 5, 4],
         ["Diana",   5, 5, 5, 5, 5, 5],
         ["Ethan",   3, 4, 2, 3, 3, 4],
         ["Fred",    4, 5, 3, 4, 5, 4],
         ["Gloria",  3, 3, 3, 4, 2, 3],
         ["Hellen",  5, 5, 4, 5, 4, 5],
         ["Ian",     4, 5, 4, 4, 3, 5],
         ["Jane",    2, 2, 2, 2, 2, 5],
         ["Kate",    3, 4, 5, 4, 5, 5]]

Let's turn this into an indexed DataFrame

In [12]:

marks_df = pd.DataFrame(marks)
marks_df.columns=["Name", "Computers", "English", "Maths", "Physics", "Chemistry", "Arts"]
marks_ix = marks_df.set_index("Name")
marks_ix

Out[12]:

	Computers	English	Maths	Physics	Chemistry	Arts
Name
Anne	5	3	5	2	4	5
Ben	5	5	5	5	5	5
Colin	4	5	3	4	5	4
Diana	5	5	5	5	5	5
Ethan	3	4	2	3	3	4
Fred	4	5	3	4	5	4
Gloria	3	3	3	4	2	3
Hellen	5	5	4	5	4	5
Ian	4	5	4	4	3	5
Jane	2	2	2	2	2	5
Kate	3	4	5	4	5	5

Computing the average mark per subject is easy: we just apply mean to each column of the table:

In [13]:

for subj in marks_ix.columns:
    print(subj, "->", round(marks_ix[subj].mean(), 2))

Computers -> 3.91
English -> 4.18
Maths -> 3.73
Physics -> 3.82
Chemistry -> 3.91
Arts -> 4.55

To compute the average mark per student we shall apply mean to the rows of the table, which we access using loc. As a warm-up let us compute the average mark for Kate:

In [14]:

print("Kate's marks:")
print(marks_ix.loc["Kate"])
print("The average mark:", round(marks_ix.loc["Kate"].mean(), 2))

Kate's marks:
Computers    3
English      4
Maths        5
Physics      4
Chemistry    5
Arts         5
Name: Kate, dtype: int64
The average mark: 4.33

The names of all the students are located in the index column, so the average mark of each student in the table can be computed like this:

In [15]:

for student in marks_ix.index:
    print(student, "->", round(marks_ix.loc[student].mean(), 2))

Anne -> 4.0
Ben -> 5.0
Colin -> 4.17
Diana -> 5.0
Ethan -> 3.17
Fred -> 4.17
Gloria -> 3.0
Hellen -> 4.67
Ian -> 4.17
Jane -> 2.5
Kate -> 4.33

7.4. Transposing a table¶

Transposing a table is an operation that swaps the rows and columns of the table so that the first row swaps with first column, the second row swaps with the secong column and so on. When transposing an indexed DataFrame the names of the columns become the index row of the new table, while the index row gives names of the columns in the new table.

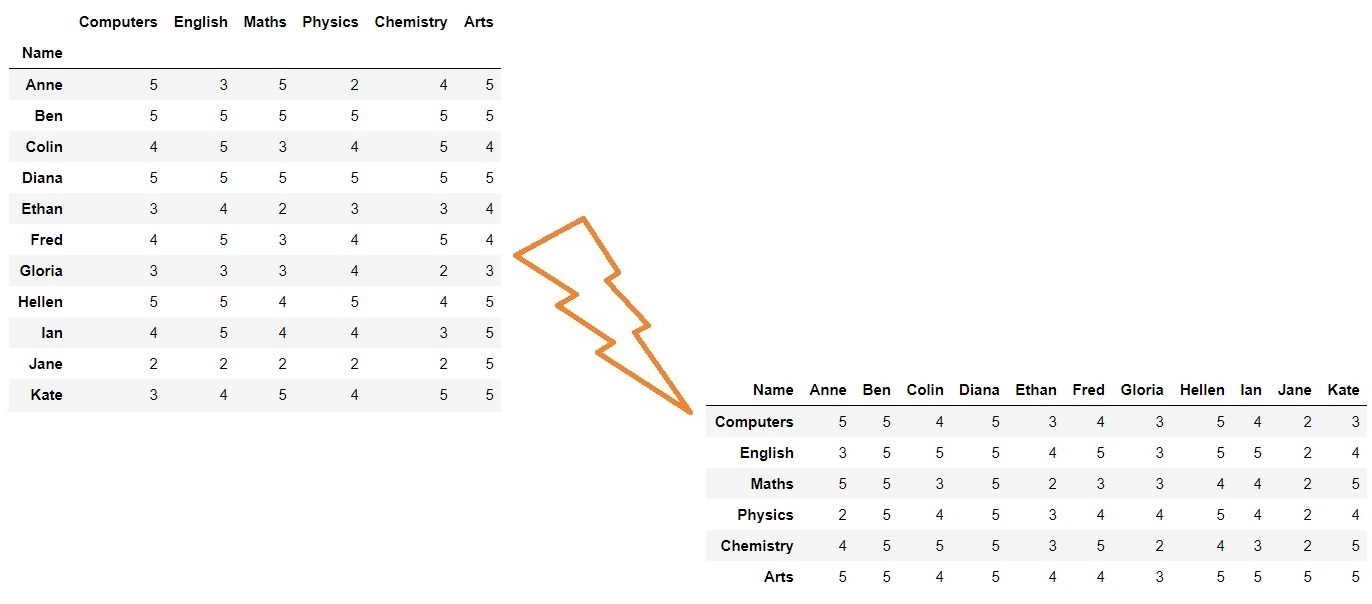
Transpose

Recall that DataFrames are optimized for efficient access to columns of the table. Therefore, it is convenient to transpose a table which has a few very long rows. Of coruse, we don't have to transpose a table to be able to work with it efficiently (since loc gives access to rows of the table), so transposing a table is a matter of taste or convenience.

To transpose a table just apply T to get the new, transposed table. For example recall that:

In [16]:

marks_ix

Out[16]:

	Computers	English	Maths	Physics	Chemistry	Arts
Name
Anne	5	3	5	2	4	5
Ben	5	5	5	5	5	5
Colin	4	5	3	4	5	4
Diana	5	5	5	5	5	5
Ethan	3	4	2	3	3	4
Fred	4	5	3	4	5	4
Gloria	3	3	3	4	2	3
Hellen	5	5	4	5	4	5
Ian	4	5	4	4	3	5
Jane	2	2	2	2	2	5
Kate	3	4	5	4	5	5

After transposing:

In [17]:

marks_tr = marks_ix.T

the new table looks line this:

In [18]:

marks_tr

Out[18]:

Name	Anne	Ben	Colin	Diana	Ethan	Fred	Gloria	Hellen	Ian	Jane	Kate
Computers	5	5	4	5	3	4	3	5	4	2	3
English	3	5	5	5	4	5	3	5	5	2	4
Maths	5	5	3	5	2	3	3	4	4	2	5
Physics	2	5	4	5	3	4	4	5	4	2	4
Chemistry	4	5	5	5	3	5	2	4	3	2	5
Arts	5	5	4	5	4	4	3	5	5	5	5

Let's check what happened to index and columns. In the original table we have:

In [19]:

marks_ix.index

Out[19]:

Index(['Anne', 'Ben', 'Colin', 'Diana', 'Ethan', 'Fred', 'Gloria', 'Hellen',
       'Ian', 'Jane', 'Kate'],
      dtype='object', name='Name')

In [20]:

marks_ix.columns

Out[20]:

Index(['Computers', 'English', 'Maths', 'Physics', 'Chemistry', 'Arts'], dtype='object')

while in the transposed table we have:

In [21]:

marks_tr.index

Out[21]:

Index(['Computers', 'English', 'Maths', 'Physics', 'Chemistry', 'Arts'], dtype='object')

In [22]:

marks_tr.columns

Out[22]:

Index(['Anne', 'Ben', 'Colin', 'Diana', 'Ethan', 'Fred', 'Gloria', 'Hellen',
       'Ian', 'Jane', 'Kate'],
      dtype='object', name='Name')

As we have already seen, the average mark per subject can be computed easily:

In [23]:

for subj in marks_ix.columns:
    print(subj, "->", round(marks_ix[subj].mean(), 2))

Computers -> 3.91
English -> 4.18
Maths -> 3.73
Physics -> 3.82
Chemistry -> 3.91
Arts -> 4.55

To compute the average marks for each student, we can use loc to access the rows of the original table, but we can alsoapply the same logic as above, but to the transposed table:

In [24]:

for student in marks_tr.columns:
    print(student, "->", round(marks_tr[student].mean(), 2))

Anne -> 4.0
Ben -> 5.0
Colin -> 4.17
Diana -> 5.0
Ethan -> 3.17
Fred -> 4.17
Gloria -> 3.0
Hellen -> 4.67
Ian -> 4.17
Jane -> 2.5
Kate -> 4.33

7.5. Exercises¶

Exercise 1. Look carefully at the code below and then answer the questions that follow:

In [25]:

import pandas as pd
students = [["Anne",    "f", 13, 46, 160],
            ["Ben",     "m", 14, 52, 165],
            ["Colin",   "m", 13, 47, 157],
            ["Diana",   "f", 15, 54, 165],
            ["Ethan",   "m", 15, 56, 163],
            ["Fred",    "m", 13, 45, 159],
            ["Gloria",  "f", 14, 49, 161],
            ["Hellen",  "f", 15, 52, 164],
            ["Ian",     "m", 15, 57, 167],
            ["Jane",    "f", 13, 45, 158],
            ["Kate",    "f", 14, 51, 162]]
students_df = pd.DataFrame(students)
students_df.columns=["Name", "Sex", "Age", "Weight", "Height"]
students_ix=students_df.set_index("Name")

temp_anomalies = pd.read_csv("data/TempAnomalies.csv", header=None)
temp_anomalies_tr = temp_anomalies.T
temp_anomalies_tr.columns = ["Year", "Anomaly"]

What is the difference between students_df and students_ix?
What does students_ix.index mean?
What is the value of students_ix.loc["Fred"]?
What is the value of students_ix.loc["Fred", "Height"]?
What is the value of students_df.loc["Fred", "Height"]?
What do you think, why did we apply T to temp_anomalies?
How many columns does temp_anomalies_tr have?

Exercise 2. This is an overview of spendings of a family over a year (in the local currency):

Item	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
Rent	8,251	8,436	8,524	8,388	8,241	8,196	8,004	7,996	7,991	8,015	8,353	8,456
Electricity	4,321	4,530	4,115	3,990	3,985	3,726	3,351	3,289	3,295	3,485	3,826	3,834
Phone (landline)	1,425	1,538	1,623	1,489	1,521	1,485	1,491	1,399	1,467	1,531	1,410	1,385
Phone (cell)	2,181	2,235	2,073	1,951	1,989	1,945	3,017	2,638	2,171	1,831	1,926	1,833
TV and Internet	2,399	2,399	2,399	2,399	2,399	2,399	2,399	2,399	2,399	2,399	2,399	2,399
Transport	1,830	1,830	1,830	1,830	1,950	1,950	1,450	1,450	1,950	1,950	2,050	2,050
Food	23,250	23,780	24,019	24,117	24,389	24,571	24,736	24,951	25,111	25,389	25,531	25,923
Rest	4,500	3,700	5,100	3,500	2,750	4,250	7,320	8,250	3,270	4,290	3,200	8,390

This table represented as a list looks like this:

In [26]:

spendings = [
  ["Rent", 8251, 8436, 8524, 8388, 8241, 8196, 8004, 7996, 7991, 8015, 8353, 8456],
  ["Electricity", 4321, 4530, 4115, 3990, 3985, 3726, 3351, 3289, 3295, 3485, 3826, 3834],
  ["Landline", 1425, 1538, 1623, 1489, 1521, 1485, 1491, 1399, 1467, 1531, 1410, 1385],
  ["Cell", 2181, 2235, 2073, 1951, 1989, 1945, 3017, 2638, 2171, 1831, 1926, 1833],
  ["TV and Internet", 2399, 2399, 2399, 2399, 2399, 2399, 2399, 2399, 2399, 2399, 2399, 2399 ],
  ["Transport", 1830, 1830, 1830, 1830, 1950, 1950, 1450, 1450, 1950, 1950, 2050, 2050],
  ["Food", 23250, 23780, 24019, 24117, 24389, 24571, 24736, 24951, 25111, 25389, 25531, 25923],
  ["Rest", 4500, 3700, 5100, 3500, 2750, 4250, 7320, 8250, 3270, 4290, 3200, 8390]
]

(a) Convert this list into a DataFrame and index it.

(b) Calculate the average spending of this family per item (Rent, Electricity etc).

Exercise 3. Five groups of students took part in a student poll about their favourite movie genres. Each student was allowed to vote for exactly one genre. The results of the poll are summarized below:

Genre	Group 1	Group 2	Group 3	Group 4	Group 5
Comedy	4	3	5	2	3
Horror	1	0	2	1	6
SF	10	7	9	8	9
Adventure	4	3	4	2	2
History	1	0	2	0	0
Romance	11	10	7	9	8

(a) COnvert this into a DataFrame indexed by genre.

(b) Compute the number of votes per genre.

(c) For each group compute the total number of students that took part in polling.

(d) What is the total number of students that took part in polling?

Exercise 4. Nutritive data for certain products in given in the table below:

Product (100g)	Nutritive value (kcal)	Carbohydrates (g)	Proteins (g)	Fats (g)
Rye bread	250	48.2	8.4	1.0
White bread	280	57.5	6.8	0.5
Cheese spread	127	4.0	3.1	10.5
Margarin	532	4.6	3.2	1.5
Yoghurt	48	4.7	4.0	3.3
Milk (2.8%)	57	4.7	3.3	2.8
Salami	523	1.0	17.0	47.0
Ham	268	0.0	25.5	18.4
Chicken breast	110	0.0	23.1	1.2

In the cell below we have converted this table into a DataFrame indexed by the product name:

In [27]:

food = pd.DataFrame([
    ["R-bread", 250, 48.2, 8.4, 1.0],
    ["W-bread", 280, 57.5, 6.8, 0.5],
    ["Spread", 127, 4.0, 3.1, 10.5],
    ["Margarin", 532, 4.6, 3.2, 1.5],
    ["Yoghurt", 48, 4.7, 4.0, 3.3],
    ["Milk", 57, 4.7, 3.3, 2.8],
    ["Salami", 523, 1.0, 17.0, 47.0],
    ["Ham", 268, 0.0, 25.5, 18.4],
    ["ChBreast", 110, 0.0, 23.1, 1.2]])
food.columns=["Product", "NutrVal", "Carbs", "Proteins", "Fats"]
food_ix = food.set_index("Product")

(a) For his breakfast Mike had two pieces of white bread and had a cup of milk. Each piece of bread had some cheese spread and a slice of ham. What is the nutritive value of Mike's breakfast (in kcal) if we assume that each piece of bread weighs 100g, that 10h of spread was used per piece of bread, that one slice of ham weighs 20g and that a cup of milk contains 200 d of milk?

(b) How much fat was there in Mike's breakfast?

(c) Visualize the amount of carohydrates in these products.

Exercise 5. The temperature anomaly is a number that tells us how much the average temperature in a particular year deviates from the optimal value. The file TempAnomalies.csv located in the folder data contains the temperature anomalies (in degrees Celsius) for the peroid of 40 years (1977-2017). The file has two rows like this:

1977,1978,1979,1980,1981,...
0.22,0.14,0.15,0.3,0.37,...

(a) Load the table into a DataFrame (Note: the table has no header so you need the header=None option in your read_scv.)

In [ ]:

(b) Transpose the table and call the two columns "Year" and "Anomaly".

In [ ]:

(c) Index the table.

In [ ]:

(d) Visualize the temperature anomalies by a line chart.

In [ ]:

Prijavi problem

Obeleži sve kategorije koje odgovaraju problemu

Još detalja - opišite nam problem

Priručnik za Džupajter

7. Indexing and transposing a table¶

7.1. Indexing¶

7.2. Accessing rows and individual cells of an indexed table¶

7.3. Computing accross rows and columns of an indexed table¶

7.4. Transposing a table¶

7.5. Exercises¶