Повећавање и смањивање објеката¶

Често цртеж желимо да прилагодимо тако што ћемо га скалирати (смањити или повећати). Ако желимо да нацртамо двоструко већи круг, потребно је навести двоструко већи полупречник, а ако је потребно нацртати двоструко већи правоугаоник, потребно је навести двоструко већи већу дужину и ширину. Испробај ово на следећем цртежу тако што ћеш смањити димензије правоугаоника на 50, а полупречник круга на 25.

Као што видиш, објекти су се смањили, али круг више није уписан у правоугаоник и цртеж не изгледа више како би требало да изгледа (центар круга и горње лево теме правоугаоника су остали непромењени). Скалирање дужи и многоуглова је још теже, јер се у њима не користе димензије, већ само координате тачака.

Дакле, да бисмо смањили или повећали цртеж, потребно је да мењамо и димензије, али и координате које одређују положај објеката. Испробај шта би се десило када би сваки од бројева који се користе приликом цртања био помножен или подељен истим бројем.

Множењем свих аргумената функција истим бројем, дакле, успешно скалирамо цртеж, међутим, цртеж уједно бива померен, што је понекад непожељно. Скалирање цртежа уз задржавање положаја генерално није једноставно учинити, међутим, у наставку ћемо видети како да цртеже направимо тако да их лако можемо и померати и скалираити.

Слово М¶

Приликом цртања слова А координате смо очитали са цртежа и директно унели у програм. Сада ћемо нацртати слово М. Да би дужи биле лепо поравнате, потребно је да две горње тачке буду на истој висини и да две доње тачке буду на истој висини, да су две леве тачке на истој ширини и да су две десне тачке на истој ширини и да је средња тачка по ширини тачно на средини између левих и десних тачака.

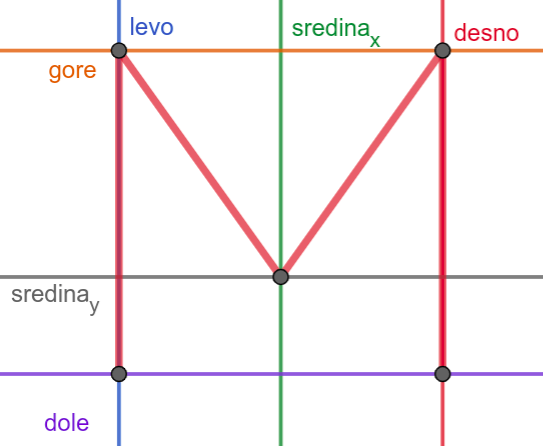
Ако мало боље проучимо положај 5 карактеристичних тачака можемо видети да све оне користе само три могуће вредности координате \(x\) (на пример, 50, 100 и 150) и само три могуће вредности координате \(y\) (на пример, 50, 120 и 150). Ове вредности можемо представити променљивама gore, dole, levo, desno, sredina_x и sredina_y, које на почетку програма иницијализујемо (постављамо) на одговарајуће вредности. Предност оваквог писања кода је у томе да ако буде потребе да се промени положај или величина слова М можемо то постићи изменом вредности променљивих којима су координате описане (промена на једном месту). Прва усправна дуж која гради слово М задата је координатама (levo, gore) и (levo, dole). Права паралелна овој дужи описана је координатама (desno, gore) и (desno, dole), а унутрашње дужи са (levo, gore), (sredina_x, sredina_y) и (desno, gore).

Можемо отићи и један корак даље и све координате израчунати само на основу положаја једне карактеристичне тачке цртежа и његове димензије. На пример, за карактеристичну тачку можемо узети тачку у средини, у којој се спајају две косе линије. Тако одабране карактеристичне тачке цртежа називају се сидра.

Сада вома једноставно можемо да променимо димензију и положај слова М. Поиграј се мало са вредношћу променљивих dim, sredina_x и sredina_y и посматрај како се мења нацртано слово. Дакле, када је цртеж нацртан релативно, у односу на неко сидро и димензију, он се лако може померати по екрану и скалирати, само тако што му се промени вредност сидра. Ово нам омогућава да цртање издвојимо у функцију која као параметре прихвата координате сидра и димензију и тако можемо лако нацртати неколико појављивања истог облика.

Облак¶

Круговима можемо нацртати и неке занимљиве облике. Нацртајмо сунце и облак на плавом небу.

Приметимо да смо облак нацртали помоћу три круга и да су координате и полупречници ових кругова задати апсолутно, помоћу конкретних бројева. Да бисмо омогућили цртање неколико облака различитог положаја и величине, потребно је да пређемо на релативно задате координате. Природно је да за сидро узмемо центар средишњег круга, а да за димензију облака узмемо његов полупречник. Из претходног примера се може видети да се полупречник мањих кругова добија множењем већег полупречника са \(\frac{5}{8}\). Такође, видимо да су центри тих кругова на истој висини као центар великог круга и да се налазе на кружници. Стога, ако претпоставимо да велики круг има центар у тачки \((x, y)\) и да му је полупречник r, тада први мали круг има центар у тачки \((x-r, y)\), а други у тачки \((x+r, y)\) и оба имају полупречник \(\frac{5r}{8}\).

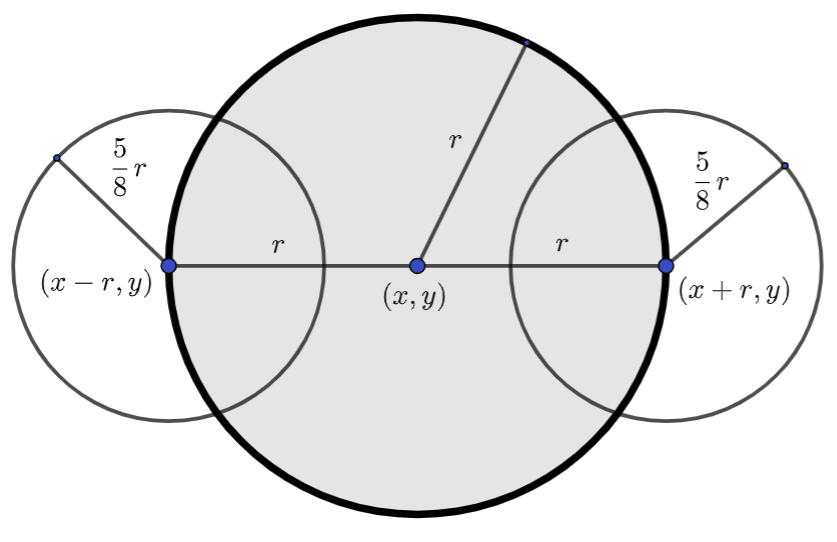
На основу овога можемо једноставно дефинисати функцију која црта облак и затим је неколико пута позвати.

Домаћи задатак - глава робота¶

Претходни програм приказује тражену главу робота. Желимо да глава буде центрирана унутар прозора. Такође, желимо да уста центрирамо хоризонтално унутар главе. Подсетимо се зато, за почетак, како то можемо нацртати правоугаоник ако су му познате координате центра (овај пут помоћу релативних координата).

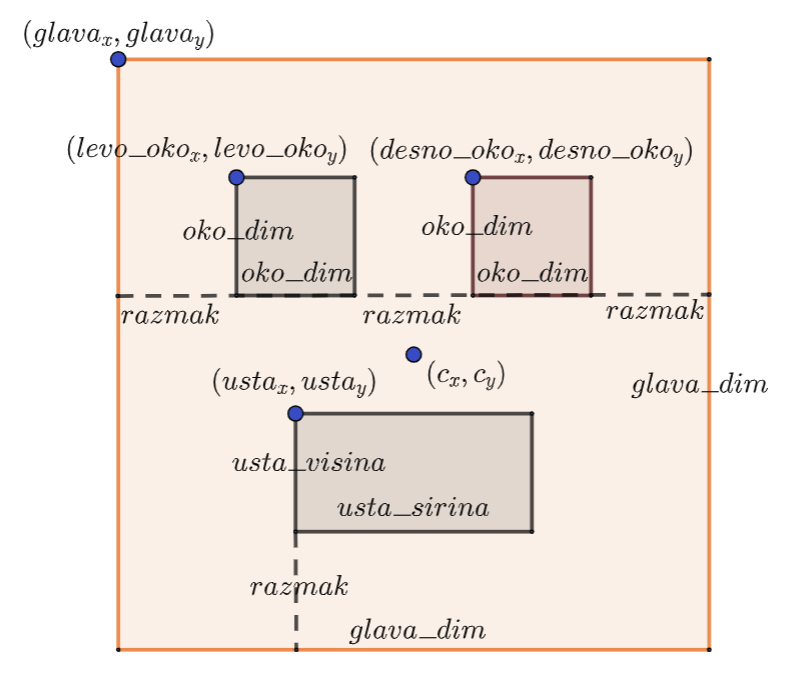
Прикажимо математичке операције којима смо израчунали све потребне координате када смо цртеж задавали у апсолутним координатама. Прозор је димензија 300 пута 300 пиксела, а глава робота 200 пута 200 пиксела. То значи да на маргине одлази по 50 пиксела и стога се горње лево теме главе робота налази у тачки са координатама \((50, 50)\). Можемо приметити да су ширина два ока и ширина размака око очију (размаци од ивице главе до очију и размак између очију) једнаки. Дакле, укупно 5 ширина ока тј. размака испуњава ширину главе робота, одакле следи да су и ширина ока и ширина размака око очију једнаке петини ширине главе, тј. 40 пиксела. Претпоставићемо да је то уједно и висина ока (јер су очи квадратног облика), као и димензија размака од горње ивице главе робота до горње ивице очију, тако да ће се горње лево теме левог ока налазити у тачки са координатама \((90, 90)\) (величина размака је додата на обе координате горњег левог темена главе), а горње лево теме десног ока налазити у тачки са координатама \((170, 90)\) (на координату \(x\) горњег левог темена левог ока која је једнака 90 додата је ширина ока од 40 пиксела и ширина размака између очију која је такође 40 пиксела). Претпоставићемо да су уста исте висине као и око, али двоструко шира од њега, да је размак од дна уста до дна главе исти као размак између врха главе и врха очију и да су уста хоризонтално центрирана. Пошто је вертикална средина екрана на линији са координатом \(x\) која је једнака 150, координате горњег левог темена уста су \((110, 170)\) (прва је добијена тако што је од координате \(x\) средине прозора одузета половина ширине уста, а друга је добијена тако што је од координате \(y\) дна уста одузета величина размака и висина уста).

Програм можемо прилагодити тако да се све координате аутоматски рачунају на основу правила које смо применили у претходној рачуници, на основу сидра (cx, cy) постављеног у средиште прозора и на основу димензије екрана. Тиме ћемо постићи да цео цртеж робота може лако да мења величину и свој положај на екрану (величина ће зависити само од димензије главе, а положај само од координата центра главе тј. сидра које је за почетак постављено у центар прозора).

Допуни наредни програм, а затим мењај димензију главе и њен центар и посматрај како се мења слика на екрану.

Домаћи задатак - Роботица Мица¶

Ако ти је претходни задатак био интересантан и желиш још мало да вежбаш рад са координатама, настави у истом духу и реши и наредни задатак.

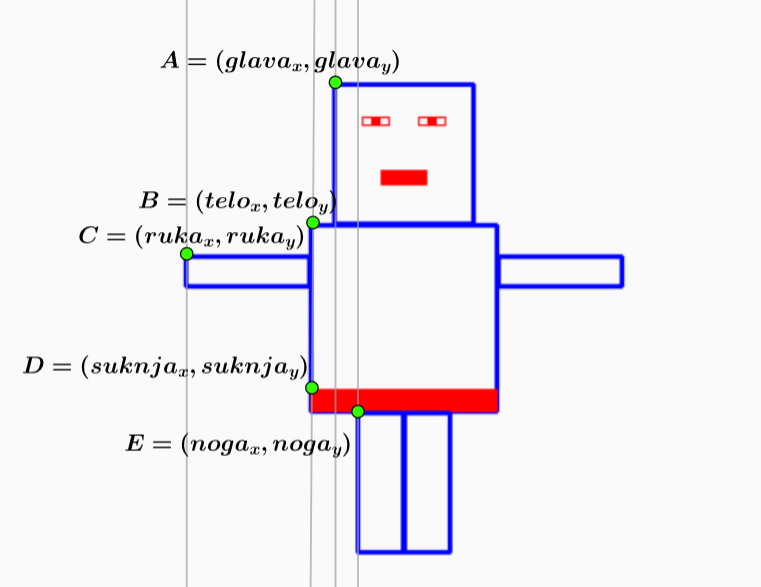
Програм је могао бити можда мало једноставнији да смо наводили апсолутне координате (конкретне бројеве), међутим, чињеница да смо све координате рачунали на основу датих координата центра и величине тела робота нам омогућава да исти програмски кôд употребимо за цртање неколиико робота. Потребно је да цртање издвојимо у функцију, чији ће параметри бити центар и димензија тела робота.