Цртање линије¶

• Корњача се на почетку налази у центру екрана и окренута је надесно (у смеру истока).

• Наредбом turtle.forward(100) корњачи говоримо да се помери напред (у смеру у ком је тренутно окренута) 100 корака и тако, пошто наша корњача подразумевано са собом носи оловку којом црта, постижемо да се на екрану нацрта дуж дужине 100 пиксела.

• Да бисмо видели јасније како корњача ради, можемо јој променити брзину кретања. turtle.speed(0) нам даје најбржу корњачу (након покретања програма се одмах види готов цртеж), док turtle.speed(10) даје најспорију корњачу (могуће је навести и било коју целобројну вредност између 0 и 10).

• Осим померања напред, корњача може да се креће и уназад, цртајући при том линију. Наредба којом се то постиже је turtle.backward.

Боја и дебљина линије¶

Могуће је поставити различите параметре који одређују начин на који се врши исцртавање.

• Да бисмо видели нашу корњачу (уместо стрелице која се подразумевано приказује) можемо употребити наредбу turtle.shape("turtle").

• Помоћу turtle.color можемо променити боју корњаче и њене оловке (и тако променити и боју трага тј. линија које се цртају). Као параметар ове наредбе у заградама под наводницима наводимо име жељене боје на енглеском језику. На пример, наредба turtle.color("red") поставља црвену боју.

• Помоћу turtle.width постављамо дебљину трага који корњача оставља, при чему се дебљина задаје као параметар. На пример, наредбом turtle.width(5) постижемо да линије које се цртају буду дебеле 5 пиксела.

Да ли можеш да погодиш шта ће се добити покретањем наредног програма? Пробај да погодиш, а онда након тога покрени програм и провери да ли си био/била у праву.

Подизање оловке¶

Корњача током свог кретања оставља траг. Међутим, некада је згодно да корњачу померимо без цртањa.

• Наредбом turtle.penup() корњача подиже своју оловку и након тога се креће по екрану не остављајући траг све док јој се не изда наредба turtle.pendown(), након чега поново почиње да оставља траг током кретања.

Допуни наредни програм тако да корњача нацрта испрекидану линију која се састоји од три дужи.

Отисци корњаче¶

• Наредбом turtle.stamp() корњача може да остави свој отисак на месту на ком се тренутно налази.

Покушај да погодиш који ће се облик добити покретањем наредног програма.

Окретање корњаче¶

• Корњача може мењати свој смер кретања тако што се окреће налево (у смеру супротном смеру кретања казаљке на сату) или надесно (у смеру кретања казаљке) за одређени број степени, за шта се користе наредбе turtle.left(n) и turtle.right(n) где је n број степени.

Покушај да погодиш који ће се облик добити покретањем наредног програма.

Резимирајмо све наредбе корњачи које смо до сада поменули.

Комплетан списак свих наредби корњаче може се наћи у званичној документацији језика Python 3.

Штриклирање¶

Квадрат¶

Квадрат се може нацртати тако што се четири пута корњачи зада да иде 100 корака напред и да се затим окрене за 90 степени (на пример, налево). Допуни наредни програм тако што ћеш додати још наредби.

За вежбу пробај да допуниш претходни програм тако да се црта шарени квадрат (сваку страницу обоји другом бојом).

Квадратни корен¶

Лого Петље¶

Напиши програм у којем корњача црта лого фондације петља. Лого се састоји од два квадрата странице 50 корака, која се додирују и окренути су 45 степени у односу на хоризонталу.

Допуни наредни програм наредбама којима се корњача окреће, тако да се добије тражена слика.

Квадрат - петља¶

Програм који исцртава квадрат можемо да скратимо ако уведемо наредбу којом постижемо да се неки задати низ наредби више пута понови. Као што смо видели, у језику Python најлакши начин да се то уради је наредба for. Као што смо већ видели, наредбу ponovi n puta можемо записати као for i in range(n):. Подсетимо се, не смемо да заборавимо двотачку, а наредбе које се понављају наводимо увучене неколико размака у односу на положај наредбе for.

Провери своје разумевање петљи тако што ћеш поређати наредбе програма у ком корњача исцртава једнакостранични троугао.

         Q-14: Поређај делове кода тако да представљају исправно решење овог задатка.import turtle
---
turtle.color("red")
---
for i in range(3):
---
   turtle.forward(100)
---
   turtle.left(120)
        

Испрекидана линија¶

Отисци корњаче¶

Правилни многоугао¶

Ако је дат број n правилни n-тоугао (правилни полигон са n страна) добијамо тако што нацртамо n његових страница. Зато је цртање странице и окретање потребно поновити n пута. Након цртања сваке странице корњача треба да се окрене тачно за величину спољашњег угла полигона. Важи да је збир свих спољашњих углова у полигону једнак 360 степени, па пошто су сви они једнаки, сваки од њих је једнак количнику бројева 360 и n. Други начин да одредимо угао за који се корњача окреће у сваком кораку је да се примети да она цртање почиње и завршава окренута ка истоку и да се у међувремену, током цртања, окреће тачно за износ једног пуног круга тј. за \(360^\circ\). Пошто се у сваком кораку окреће подједнако, окрет износи тачно \(\frac{360^\circ}{n}\). У програмском језику Python, количник бројева a и b можемо израчунати помоћу a / b (више речи о томе биће речено у поглављу о аритметичким операцијама и дељењу), па број \(\frac{360}{n}\) можемо израчунати помоћу 360 / n.

Као и у претходним случајевима, твој задатак је да исправиш грешке у следећем програму.

Збир унутрашњих углова сваког n-тоугла (у Еуклидској геометрији) једнак је вредности \((n-2)\cdot 180^\circ\). Заиста, ако из неког темена конвексног многоугла повучемо све његове дијагонале оне ће га поделити на укупно \(n-2\) троугла (на наредној слици, петоугао је на тај начин подељен на три троугла).

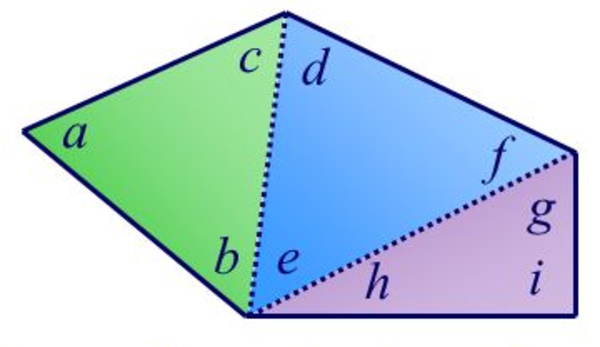
Збир углова у сваком троуглу (у Еуклидској геометрији) је \(180^\circ\). Сваки унутрашњи угао полигона једнак је збиру неколико углова тих троуглова, док је сваки унутрашњи угао троугла део тачно једног од унутрашњих углова полигона, па је укупан збир унутрашњих углова полигона једнак укупном збиру углова тих троуглова, а то је тачно \((n-2)\cdot 180^\circ\).

Сваки спољашњи угао полигона је допуна унутрашњег угла до \(180^\circ\) степени (његов суплемент). Пошто је тих углова \(n\) важи да је збир спољашњих углова једнак разлици броја \(n \cdot 180^\circ\) и збира унутрашњих углова полигона, који је, на основу претходног, једнак \((n-2)\cdot 180^\circ\). Зато је збир спољашњих углова полигона једнак \(n\cdot 180^\circ - (n-2)\cdot 180^\circ\), што је тачно \(360^\circ\).

Звезда¶

Звезда са пет кракова се састоји од централног правоуглог петоугла на чијим се ивицама налазе једнакостранични троуглови. Збир унутрашњих углова у правилном петоуглу је \((5-2)\cdot 180^\circ\) тако да је сваки угао једнак \(108^\circ\). Ако посматрамо углове на базама два суседна крака (једнакостранична троугла) видимо да су они унакрсни и да заједно са углом од \(108^\circ\) и са њему унакрсном углом чине пун угао. Стога је сваки угао на основици крака једнак \(\frac{360^\circ - 2 \cdot 108^\circ}{2} = 72^\circ\). Пошто је збир углова у краку једнак \(180^\circ\), угао при врху крака једнак је \(180^\circ - 2 \cdot 72^\circ = 36^\circ\). Та информација нам је кључна да бисмо могли да нацртамо звезду. Звезду ћемо цртати тако што ћемо пет пута нацртати дуж од 100 корака и затим се окренути тако да наредна дуж заклопи угао од \(36^\circ\) са претходном. Да бисмо то постигли, корњача треба да се окрене надесно за суплемент тог угла тј. за угао од \(180^\circ - 36^\circ = 144^\circ\).

Теби препуштамо да на основу ове дискусије допуниш наредни програм.

Слово L¶

Слово И¶

Плаво-црвена линија¶

Отисци корњаче у теменима n-тоугла¶