Појам функције¶

Функције су један од основних појмова математике и програмирања. Оне представљају пресликавања одређених улазних вредности (каже се параметара, аргумената) у једну или више излазних вредности тј. резултата. На пример, функција може да као улазни параметар добије дужину странице једнакостраничног троугла \(а\) и да као резултат врати дужину обима тог троугла \(3\cdot a\). Таква зависност би се у математици описала као \(f(a) = 3\cdot a\) што значи да функција коју смо назвали f (што је најчешће име за функцију) на основу датог параметра \(а\) одређује вредност \(3\cdot a\). Слично, функција која израчунава обим правоугаоника на основу дужине његових страница би се у математици описала као \(g(a, b) = 2\cdot a + 2 \cdot b\). У овом случају је функцији дат назив \(g\), она има два улазна параметра (\(a\) и \(b\)) и враћа резултат који је одређен формулом \(2\cdot a + 2 \cdot b\).

Касније ћемо видети како можемо дефинисати функције у језику Python, а започетак ћемо се само позабавити коришћењем неких основних уграђених функција (оне су већ дефинисане језиком и можемо их слободно користити тј. позивати у нашим програмима). У наставку ћемо детаљније описати следеће функције:

• min, max - минимум и максимум

• abs - апсолутна вредност

• math.pow, math.sqrt - степен, квадратни корен

• round, math.floor, math.ceil - заокругљивање реалних бројева

Минимум и максимум¶

У многим задацима потребно је одредити мањи или већи од два дата броја. Пошто је тај задатак веома чест, програмски језик Python нуди решење у виду функција min и max. На пример, вредност израза min(2, 5) је мањи од бројева 2 и 5 тј. број 2 (тај израз представља позив функције min са аргументима 2 и 5), док је вредност израза max(2, 5) већи од бројева 2 и 5 тј. број 5 (тај израз представља позив функције max са аргументима 2 и 5).

Минимум и максимум неколико бројева могуће је израчунати тако што се сви наведу као параметри функција min тј. max. На пример, вредност израза max(3, 2, 5, 4) је 5.

Покажимо сада неколико задатака у чијем нам решењу ове функције могу помоћи.

Браћа и књиге на полици¶

Аљоша и Борис су браћа која иду у трећи и шести разред и деле исту собу. У соби имају две полице за књиге, међутим, књиге су им се измешале и они желе да их раздвоје тако да на једној полици буду само Аљошине књиге за трећи, а на другој полици буду само Борисове књиге за шести разред (свеједно им је која ће полица бити чија). Колики је најмањи број књига које треба да помере?

Приметимо да постоје два начина да се књиге раздвоје. Први је да се све Аљошине књиге са прве полице пребаце на другу, а да се све Борисове књиге са друге полице пребаце на прву полицу. Други начин је да се све Борисове књиге са прве полице пребаце на другу, а да се све Аљошине књиге са друге полице пребаце на прву. У првој варијанти број књига које се пребацују једнак је збиру броја Аљошиних књига на првој и Борисових књига на другој полици, док је у другој варијанти тај број једнак збиру броја Борисових књига на првој и Аљошиних књига на другој полици. Решење је мањи од та два броја (а мањи од два броја можемо израчунати функцијом min).

# -*- acsection: general-init -*- # -*- acsection: var-init -*- polica1_aljosine = 10 polica1_borisove = 5 polica2_aljosine = 7 polica2_borisove = 8 # -*- acsection: main -*- potrebno_premestiti = 0 # ispravi ovaj red # -*- acsection: after-main -*- print(potrebno_premestiti) ==== from unittest.gui import TestCaseGui class myTests(TestCaseGui): def testOne(self): for polica1_aljosine, polica1_borisove, polica2_aljosine, polica2_borisove, potrebno_premestiti in [(8, 4, 2, 6, 6), (9, 10, 11, 7, 16), (4, 2, 3, 6, 5)]: self.assertEqual(acMainSection(polica1_aljosine = polica1_aljosine, polica1_borisove = polica1_borisove, polica2_aljosine = polica2_aljosine, polica2_borisove = polica2_borisove)["potrebno_premestiti"],potrebno_premestiti,"Ако на првој полици Аљоша има %s, а Борис %s књига, а на другој Аљоша %s, а Борис %s, тада је потребно преместити %s." % (polica1_aljosine, polica1_borisove, polica2_aljosine, polica2_borisove, potrebno_premestiti)) myTests().main()

polica1_aljosine = 10 polica1_borisove = 5 polica2_aljosine = 7 polica2_borisove = 8 potrebno_premestiti = min(polica1_aljosine + polica2_borisove, polica1_borisove + polica2_aljosine) print(potrebno_premestiti)

Апсолутна вредност¶

Још једна веома корисна функција коју си упознао/упознала у математици је апсолутна вредност. Апсолутном вредношћу се одређује одступање броја од нуле. На пример, број 4 одступа од нуле за 4, док број -5 одступа од нуле за 5 јединица. Дакле апсолутна вредност броја \(x\), која се, подсетимо се обележава са \(|x|\), једнака самом броју \(x\) ако је \(x \geq 0\) тј. броју \(-x\), ако је \(x < 0\).

У језику Python апсолутну вредност можемо израчунати помоћу функције abs. Тако је вредност израза abs(5) једнака 5, док је вредност израза abs(-3) једнака 3.

Једна од најзначајнијих примена апсолутне вредности је да се израчуна удаљеност бројева, без обзира на њихов међусобни однос. Наиме, растојање између бројева \(x_1\) и \(x_2\) је једнако апсолутној вредности њихове разлике тј. вредности \(|x_1 - x_2|\), без обзира да ли је \(x_1 \geq x_2\) или је \(x_1 < x_2\). Размотримо наредни задатак.

Менхетн растојање¶

Менхетн, део града Њујорка је организован у авеније у правцу север-југ и улице у правцу isток-запад. Размак између две улице је 80m, а између две авеније је 275m. Ако се Том налази на углу улице \(u_1\) и авеније \(a_1\) и жели да стигне на угао улице \(u_2\) и авеније \(a_2\), колико ће метара морати да пређе.

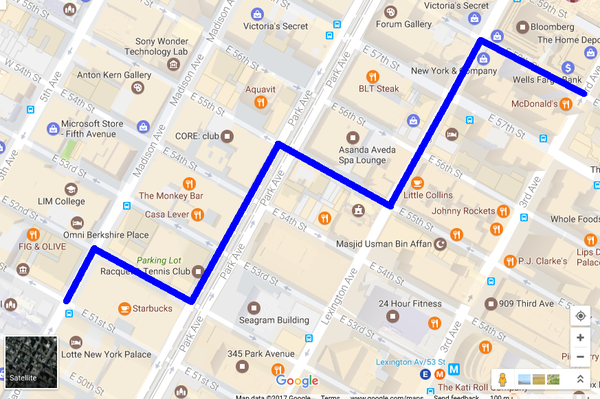
Том има више начина да стигне са једног на друго место (може да иде цик-цак, на разне начине), међутим, пређено растојање је исто као када би прво ишао улицом \(u_1\) све док не дође до угла са авенијом \(a_2\), а затим да се креће авенијом \(а_2\) све док не дође до угла са улицом \(u_2\). Дакле, потребно је израчунати растојање између авенија \(a_1\) и \(a_2\) (да би се оно добило у метрима потребно је помножити апсолутну разлику између њихових редних бројева размаком између суседних авенија) и на то додати растојање између улица \(u_1\) и \(u_2\) (да би се оно добило у метрима потребно је помножити апсолутну разлику између њихових редних бројева размаком између суседних улица).

Исправи наредни код тако да коректно израчуна пређени пут (наравно, програм треба да ради и када се улазни подаци промене или учитају са улаза).

# -*- acsection: general-init -*- # -*- acsection: var-init -*- razmak_ulica = 80 razmak_avenija = 275 ulica1 = 51 avenija1 = 6 ulica2 = 58 avenija2 = 3 # -*- acsection: main -*- rastojanje = abs(avenija1 - avenija2) * 0 + \ 0 * razmak_ulica # -*- acsection: after-main -*- print(rastojanje) ==== from unittest.gui import TestCaseGui class myTests(TestCaseGui): def testOne(self): for (ulica1, avenija1, ulica2, avenija2, razmak_ulica, razmak_avenija, rastojanje) in [(3, 5, 8, 4, 80, 275, 675), (1, 7, 2, 4, 80, 275, 905), (9, 4, 11, 2, 80, 275, 710), (4, 8, 1, 5, 80, 275, 1065)]: self.assertEqual((acMainSection(ulica1 = ulica1, avenija1 = avenija1, ulica2 = ulica2, avenija2 = avenija2, razmak_ulica = razmak_ulica, razmak_avenija = razmak_avenija)["rastojanje"]), rastojanje , "Растојање између тачака (%s, %s) и (%s, %s) је %s." % (ulica1, avenija1, ulica2, avenija2, rastojanje)) myTests().main()

Приметимо да је формула у претходном примеру била веома дугачка и проценили смо да је прегледније да је одштампамо кроз више редова. Да бисмо нагласили да се нека наредба наставља и у следећој линији на крај линије стављамо симбол \.

ulica1 = 51 avenija1 = 6 ulica2 = 58 avenija2 = 3 razmak_ulica = 80 razmak_avenija = 275 rastojanje = abs(avenija1 - avenija2) * razmak_avenija + \ abs(ulica1 - ulica2) * razmak_ulica print(rastojanje)

Краљево растојање на шаховској табли¶

Краљ се на шаховској табли налази на пољу обележеном координатама \((x_1, y_1)\). Ако се зна да се у сваком потезу краљ може кретати по једно поље у било ком од осам смерова, израчунај колики је најмањи број потеза потребних да краљ стигне на поље означено координатама \((x_2, y_2)\).

Овај задатак је донекле сличан претходном. Поново је потребно да израчунамо хоризонтално и вертикално растојање између полазне и долазне тачке. Размисли како се број потеза може израчунати на основу та два растојања (у првих неколико потеза краљ може да се креће дијагонално, а после тога, ако је потребно, наставиће да се креће хоризонтално тј. вертикално). Допуни дефиницију функције која израчунава број потеза краља између поља (x1, y1) и (x2, y2).

def kralj(x1, y1, x2, y2): broj_poteza = 0 # na ovom mestu izracunaj broj poteza return broj_poteza ==== from unittest.gui import TestCaseGui class myTests(TestCaseGui): def testOne(self): self.assertEqual(kralj(3, 8, 5, 2), 6, "Ако краљ треба да стигне са поља (3, 8) на поље (5, 2) потребно му је 6 потеза.") self.assertEqual(kralj(7, 4, 3, 7), 4, "Ако краљ треба да стигне са поља (7, 4) на поље (3, 7) потребно му је 4 потеза.") self.assertEqual(kralj(1, 8, 8, 1), 7, "Ако краљ треба да стигне са поља (1, 8) на поље (8, 1) потребно му је 7 потеза.") self.assertEqual(kralj(5, 5, 2, 2), 3, "Ако краљ треба да стигне са поља (5, 5) на поље (2, 2) потребно му је 3 потеза.") myTests().main()

Хоризонтално и вертикално растојање израчунавамо као апсолутну вредност разлике одговарајућих координата. Број дијагоналних потеза једнак је мањем од два растојања, док је број хоризонталних тј. вертикалних потеза након тога једнак разлици између већег и мањег растојања. Дакле, укупан број потеза је једнак већем од два растојања. Заиста, у почетним потезима се оба растојања умањују за по један, све док мање растојање не достигне нулу, након чега дуже растојање наставља да се умањује за један и укупан број потеза да оно достигне нулу једнак је његовој полазној вредности.

x1 = 3 y1 = 8 x2 = 5 y2 = 2 broj_poteza = max(abs(x1 - x2), abs(y1 - y2)) print(broj_poteza)

Остале математичке функције¶

Поред ових које смо видели, језик Python 3 нуди многе друге корисне функције за рад са бројевима. На пример, функција round заокружује дати реални број на најближи цео број.

Слично, функција math.ceil заокружује дати реалан број навише тј. на најмањи цео број већи или једнак њему, док math.floor заокружује дати реалан број наниже тј. на највећи цео број мањи или једнак њему. На пример, math.ceil(2.1) је 3, исто као и math.ceil(2.9), док је math.floor(2.1) једнако 2, исто као и math.floor(2.9). Приметимо да имена ових функција почињу са math. Оне су део такозване математичке библиотеке и да би се могле користити у програму на његовом почетку мора бити написано import math.

Функција math.sqrt израчунава квадратни корен тј. онај ненегативан број који када се помножи сам са собом (када се квадрира) даје полазни број. На пример, важи да је \(2 \cdot 2 = 4\), тако да је квадратни корен броја \(4\) број \(2\) (то се у математици записује као \(\sqrt{4} = 2\).

Пошто важи да је \(P = a\cdot a\), важи да је \(a = \sqrt{P}\).

Функција math.pow врши степеновање. На пример, \(2^{8} = 256\) се може израчунати помоћу math.pow(2, 8). Као што множење означава узастопно сабирање, тако степеновање означава узастопно множење. Други степен броја \(2\) je \(2^2 = 2 \cdot 2 = 4\), трећи степен броја \(2\) је \(2^3 = 2 \cdot 2 \cdot 2 = 8\) и тако даље. Поменимо и да је степен дефинисан и када аргументи нису цели бројеви, али се тиме нећемо бавити. Степеновање се може израчунати и оператором **. Тако се уместо math.pow(2, 8) може употребити израз 2 ** 8 чија је вредност такође 256.

Осим функција, у библиотеци math дефинисане су и разне корисне константе. На пример, број \(\pi\) који представља однос пречника и обима круга доступан је помоћу math.PI (вредност тог броја је око \(3,141592\)).

Примери дефинисања функција¶

На пример, функција која израчунава обим правоугаоника се може дефинисати и онда употребити на следећи начин.

Дефиниција функције почиње речју def након тога се наводи назив функције, затим у заградама наведени улазни параметри функције и симбол двотачка (:). Након те прве линије наводи се тело функције, које мора бити мало увучено. Код најједноставнијих функција (као што су ове две наведене у примерима) тело функције представља само наредба return након које се налази израз који представља везу између улазних параметара и резултата функције. Код компликованијих функција у телу се налазе дужа израчунавања, али се и даље у телу функције (најчешћње на самом крају) налази наредба return иза које се наводи вредност функције (то може бити и име променљиве у којој је израчуната резултујућа вредност). Функције се позивају тако што се наведе њихов назив и у загради вредности аргумената.

Површина сложених облика¶

Размотримо проблем израчунавања површине наредних сложених облика.

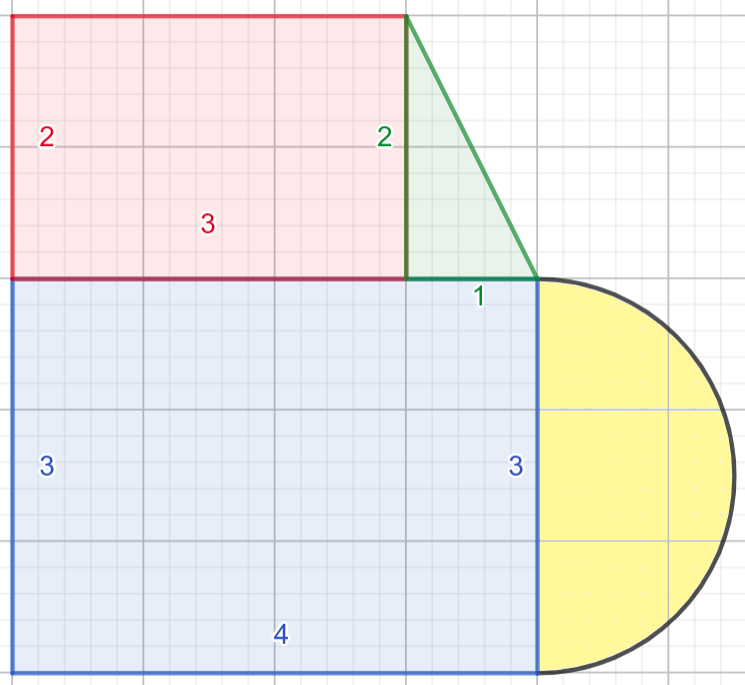
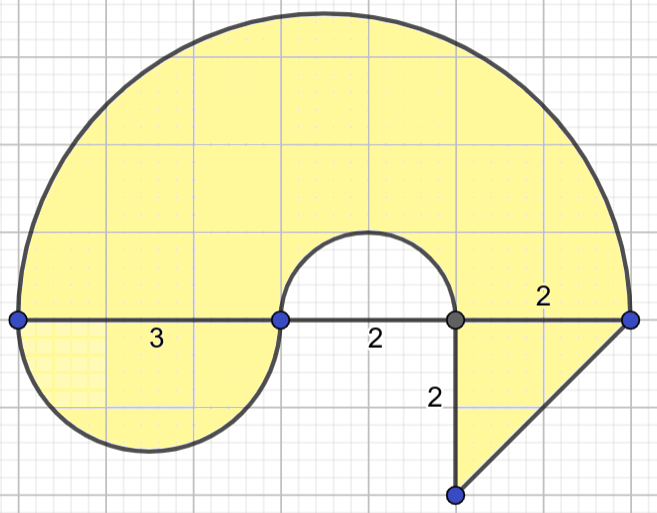
Први облик се може разложити на два правоугаоника, један правоугли троугао и један полукруг, док се површина другог облика може добити тако што се од површине највећег полукруга одузме површина најмањег, а дода површина средњег полукруга и површина правоуглог троугла.

Ако једном дефинишемо функције за израчунавање површине сваког од тих елементарних облика, веома једноставно у главном програму можемо израчунавати површине разних сложених облика, не размишљајући више о формулама потребним за израчучнавање површине појединачних облика (површина правоугаоника страница \(a\) и \(b\) израчунава се по формули \(P=a\cdot b\), површина правоуглог троугла чије су странице које образују прав угао \(a\) и \(b\) једнака је \(\frac{a\cdot b}{2}\), јер је тај троугао половина одговарајућег правоугаоника, а површина круга полупречника \(r\) може се израчунати по формули \(P = r^2\pi\), где је \(pi = 3,1415926...\), а у језику Python се може добити помоћу math.pi).

# površina pravougaonika datih stranica def P_pravougaonika(a, b): return a * b # površina pravouglog trougla datih kateta def P_pravouglog_trougla(a, b): return a * b / 2 # površina kruga datog poluprečnika def P_kruga(r): return r * r * math.pi # površina polukruga datog prečnika def P_polukruga(R): return P_kruga(R / 2) / 2 P1 = (P_pravougaonika(2, 3) + ??? + P_pravouglog_trougla(2, 1) + P_polukruga(3)) P2 = (P_polukruga(7) - P_polukruga(2) + ??? + P_pravouglog_trougla(???, ???)) print(P1, P2)

Функције са више резултата¶

У неким ситуацијама функција треба да врати више вредности. На пример, желимо да претварање центиметара у метре и центиметре опишемо у облику посебне функције. Резултат тада можемо вратити у облику пара или торке елемената (више речи о паровима и торкама је дато у поглављу о представљају података у програмима).

Сврха дефинисања функција¶

Резимирајмо на крају неколико основних разлога за дефинисање функција.

• Увођењем функција добијају се разумљивији програми (ономе ко чита главни програм много је јасније да се у неком делу израчунава обим правоугаоника ако у програму види израз obim_pravougaonika(2, 5) него ако види израз 2 * 2 + 2 * 5)). Када дефинишемо погодне функције, главни програм је било много лакше написати.

• Функције помажу да се програм скрати тако што се избегава понављање истог програмског кода (ако је тај програмски код дугачак и компликован, издвајање у функцију може значајно поједноставити и скратити програм). Ако се покаже да је тај део кода често потребно мењати (што је често случај у програмирању) то што се код јавља само једном (у склопу тела функције) чини одржавање много једноставнијим (не морамо измене да правимо на пуно места, већ само на једном).

• Функције помажу и да се неки проблеми реше, тако што омогућавају разлагање комплексних проблема на једноставније потпроблеме.

Домаћи задатак¶

Уради за домаћи неколико наредних задатака.