Час 10 - цртање у петљама - утврђивање¶
На овом часу додатно увежбај цртање уз помоћ петљи тако што ћеш урадити још неколико задатака из ове области. Не мораш да урадиш све задатке, већ само одабери оне који ти се из неког разлога највише допадају. Пожељно је да сваки задатак урадиш самостално, од почетка до краја. Тек ако из више покушаја не успеш, онда потражи помоћ, па покушај да допуниш код. Ако ни то не успеш, онда погледај коначно решење.
Испрекидана линија¶
Напиши програм који по средини екрана исцртава испрекидану линију код које је свака линијица обојена насумично одабраном бојом. Дужине линијица и размак између њих су једнаки 30 пиксела, а дебљина линије је 5 пиксела.
Шпартање дијагоналама¶
У једном од претходних задатака шпартали смо прозор водоравним и усправним линијама. Тада смо видели да се крајње тачке тих линија налазе на ободу прозора и имају координате облика \((i\cdot d_x, 0)\), \((i\cdot d_x, v)\), \((0, i\cdot d_y)\) и \((s, i\cdot d_y)\), где су \(d_x\) и \(d_y\) хоризонтално тј. вертикално растојање између две линије, док су \(s\) и \(v\) ширина тј. висина прозора. Ако употребимо исте тачке, али их спојимо дужима на мало другачији начин, можемо добити веома интересантне шаре.
Напиши програм који дијагонално шпарта прозор у правцу споредне дијагонале. Број линија изнад споредне дијагонале (укључујући и њу) је \(n=10\) (исто важи и за број линија испод споредне дијагонале).
Крајње тачке ових дужи деле сваку од ивица прозора на по \(n\)
једнаких делова. Стога се растојање \(d_x\) између суседних тачака
на горњој (и доњој) ивици прозора може израчунати дељењем ширине, а
растојање \(d_y\) између суседних тачака на левој (и десној) ивици
дељењем висине прозора бројем \(n\). Посматрајмо дужи које спајају
леву и горњу ивицу прозора (последња таква је споредна
дијагонала). Прва дуж спаја тачке са координатама \((d_x, 0)\) и
\((0, d_y)\), друга дуж тачке са координатама \((2 d_x,
0)\) и \((0, 2 d_y)\) итд. Дакле, те дужи можемо нацртати тако
што у петљи у којој бројачка променљива i мења вредности од 1 до
n цртамо дужи које спајају тачке са координатама (i*dx, 0) и
(0, i*dy). Слично, прва дуж испод дијагонале спаја тачке са
координатама \((w, d_y)\) и \((d_x, h)\), друга тачке са
координатама \((w, 2 d_y)\) и \((2 d_x, h)\) итд.,
где \(w\) означава ширину, а \(h\) висину екрана. Дакле, те
дужи можемо нацртати тако што у петљи у којој бројачка променљива
i мења вредности од 1 до n-1 цртамо дуж која спаја тачке са
координатама (sirina, i*dy) и (i*dx, visina).
На основу претходне дискусије напиши наредни програм.
Програм се може мало једноставније написати ако се не обазиремо на то да крајње тачке дужи изађу ван граница прозора.
Ажурирај претходни програм тако да се додају и дијагонале паралелне главној дијагонали исцртане црвеном бојом.
Шарање ротираним дужима¶
Напиши програм који исцртава шару по прозору која је креирана од дужи, како је приказано на слици.
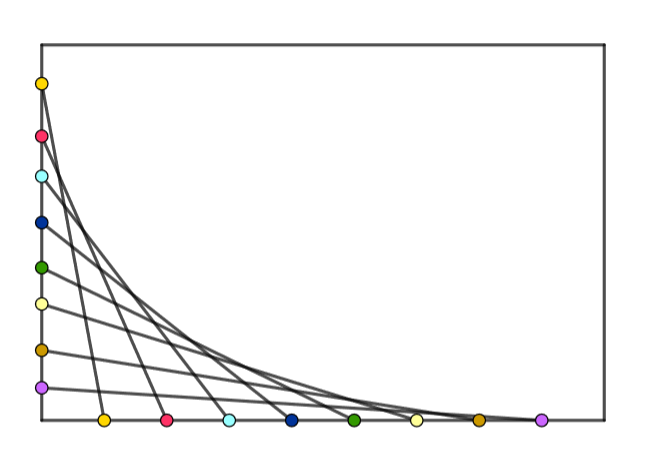
Иако шара изгледа на први поглед прилично различито, овај програм је
заправо прилично сличан претходном. Прва дуж спаја тачке се
координатама \((0, d_y)\) и \((d_x, h)\), друга спаја тачке са
координатама \((0, 2d_y)\) и \((2d_x, h)\), итд., све до дужи
која спаја тачке \((0, (n-1)\cdot d_y)\) и \(((n-1)\cdot d_x,
h)\), где је \(h\) висина прозора. Дакле, дужи можемо нацртати у
петљи у којој се бројачка променљива i креће од 1 до n-1,
у чијем телу цртамо дуж која спаја тачке са координатама (0, i*dy)
и (i*dx, visina). Ако би се бројач у петљи мењао од 0 до
n, тада би се цртале и прва вертикална и последња хоризонтална дуж
(oне се не виде, јер се поклапају са ивицама прозора).
На основу претходне дискусије допуни наредни програм.
Допуни претходни програм тако да се сличан шаблон понавља у сва четири угла прозора, како је приказано на слици.
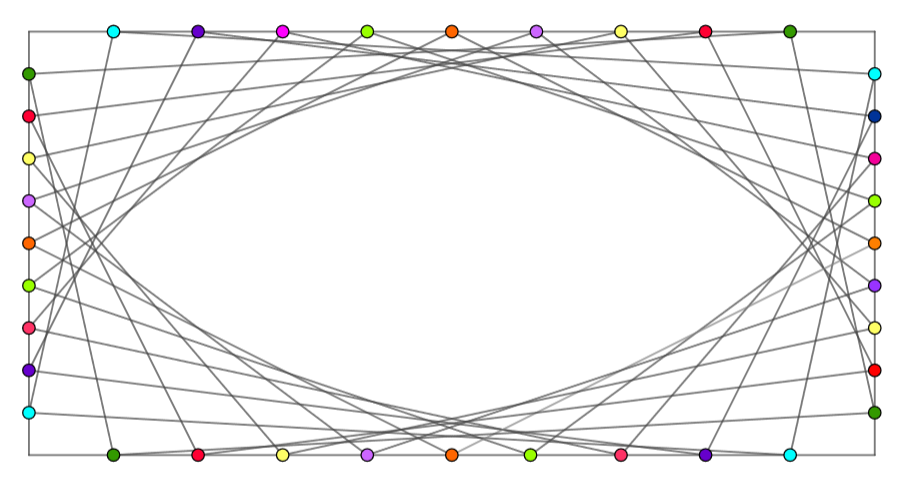
Пажљиво анализирај координате крајњих тачака дужи, уочи правилности, експериментиши и покушај тако да дођеш до решења.
Решење се може добити на следећи начин.
Крешендо¶
Напиши програм који исцртава 100 паралелних вертикалних линија равномерно распоређених ширином прозора, тако да дужина тих линија равномерно расте од нуле па до висине прозора.
Лоптице¶
Напиши програм који исцртава лоптице хоризонтално распоређене по средини екрана, који се међусобно додирују, тако да је полупречник прве 10 пиксела, а полупречник сваке наредне за 10 пиксела већи од претходне. Лоптице су наизменично црвене, зелене, плаве и жуте боје (и тако у круг).
Згуснуте линије¶
Нацртај цртеж у ком се усправне линије полако разређују како се померамо ка десној страни прозора.
Цигле¶
Редови цигала наизменично почињу целом циглом и половином цигле. Нека
је ширина цигле означена са \(s\), а њена висина са
\(v\). Целу циглу на почетку реда добијамо тако што цртамо
правоугаоник од тачке на датој висини, са \(x\) координатом
једнаком нули. Половину цигле на почетку реда можемо да добијемо тако
што нацртамо целу циглу померену за \(s \over 2\) улево, то јест
тако што цртамо правоугаоник од такче на истој висини, али са
\(x\) координатом једнаком -s // 2. Тако постижемо да се види
само десна половина цигле. Остаје да решимо када цртамо померену циглу
а када не.
Једно решење је да место почетка реда цигала чувамо у променљивој,
назовимо је x_poc. После сваког исцртаног реда, проверавамо да ли
променљива x_poc има вредност нула или -s // 2. Коју год
од ове две вредности променљива имала, доделићемо јој ону другу
вредност, да би у следећем реду цртање цигала почело другачије.
Нагласимо да корак у петљи мора бити целобројна вредност тако да пола ширине цигле морамо израчунати целобројним дељењем.
Тараба¶
Напиши програм који црта сеоску ограду (тарабу).
Сваку притку ограде представићемо у облику многоугла. Да бисмо притке могли да цртамо на различитим позицијама, потребно је да координате тог многоугла буду задате релативно. Пошто ће све притке бити увек на истој висини (истој \(y\) координати), довољно је да притке буду параметризоване једним параметром - координатом \(x\) левог краја притке.
Један начин је да у задавању темена притке користимо променљиву x,
која се мења у петљи. Када би се притке померале и на горе или на
доле, онда би у задавању темена учествовала и променљива y.
Можемо и да уведемо функцију која црта притку у односу на њену релативно задату \(x\) координату.
Још једна могућност је да приликом цртања пресликамо координате основне листе (коришћењем компрехенсије тј. скуповне нотације за листе).
Коришћењем било ког од наведених решења нацртај тарабу.

