Час 7 - понављање облика коришћењем петљи¶
Цртање у петљи¶
Концентрични кругови¶
Напиши програм који црта концентричне кругове чији је центар у центру екрана, а полупречници су редом 10, 20, …, 100 пиксела. Сваки круг нацртати црвеном линијом дебљином 5 пиксела.
Центар прозора се једноставно израчунава тако да му је координата x на пола ширине, а координата y на пола висине прозора (обрати пажњу на то да се код кругова морају користити цели бројеви, па стога морамо употребити целобројно дељење). Након тога, можемо навести 10 наредби за цртање кругова.
Претходно решење има пуно мана. За почетак, тешко је откуцати оволики број наредби. Даље, ако бисмо се предомислили и променили број кругова или величине полупречника, програм би захтевао доста компликоване измене. Задатак се много боље и једноставније решава када се примети да се полупречници кругова редом мењају од 10 до 100 са кораком 10 (10, 20, 30, …, 90, 100) и када се подсетимо да у Пајтону такво набрајање може остварити петљом:
Пошто десни крај није укључен у набрајање (узимају се вредности из полуотвореног интервала \([pocetak, kraj)\)), да би последњи полупречник био 100, за крај је потребно навести вредност 101.
На основу претходне дискусије допуни наредни програм.
Мердевине¶
Измените наредни програм тако да се пречаге мердевина цртају у петљи.
Пажљиво проучи које се вредности мењају кроз позиве функције
pg.draw.line, шта је почетна вредност, шта је крајња вредност и
који је корак, па на основу тога позови функцију range у оквиру
петље for.
Једно могуће решење је:
Правилно распоређени бројеви¶
У оба претходна примера било је потребно да набројимо неки низ правилно распоређених бројева. У задатку са круговима то су били бројеви 10, 20, …, 100, а у задатку са мердевинама то су били бројеви 50, 100, 150, 200, 250.
У решењима задатка видели смо да је један начин да се то уради петља облика
при чему је било потребно обратити пажњу на то да десни крај није укључен у набрајање (узимају се вредности из полуотвореног интервала \([x_0, x_{Max}+1) = [x_0, x_{Max}]\)).
Провери да ли ово разумеш тако што ћеш одговорити на следеће питање.
-
Упари низ бројева са петљом која га генерише.
Покушај поново!
- 15, 30, 45, 60, 75
- for i in range(15, 75+1, 15)
- 100, 350, 600
- for i in range(100, 600+1, 250)
- 5, 10, 15, 20, 25, 30
- for i in range(5, 30+1, 5)
- 100, 200, 300, 400, 500, 600
- for i in range(100, 600+1, 100)
Наведимо још неколико начина да се исти ефекат постигне. Ако почетак обележимо са \(x_0\), а корак са \(d_x\), тада су вредности које исписујемо \(x_0\), \(x_0 + d_x\), \(x_0+2d_x\), \(x_0+3d_x\) итд. Ако желимо да набројимо \(n\) ових вредности, тада можемо употребити петљу облика
Још један начин је да променљиву x ажурирамо кроз сваки корак петље, тако што је увећавамо за dx.
Видећемо да се велики број задатака са цртањем правилно распоређених облика може решити применом оваквих петљи.
Нагласимо још и да функција range са кораком (са три аргумента)
прима обавезно целобројне аргументе, па у ситуацијама када корак није
целобројан њено коришћење није могуће.
Хоризонтално и вертикално распоређивање облика¶
Често у применама имамо потребу да распоредимо објекте тако да буду један до другога, тако да су сви објекти равномерно распоређени, тј. тако да су свака два узастопна објекта на истом растојању.
Хоризонтално распоређени кругови¶
Нацртај 10 кругова пречника 30 пискела тако да буду равномерно распоређени ширином екрана и да се међусобно додирују.
Наредних пар питања ће ти помоћи да решиш овај задатак.
- 2*r
- Тачно
- r
- Покушај поново
- r / 2
- Покушај поново
- 100
- Покушај поново
Q-42: Ако се два круга полупречника \(r\) додирују, тада је растојање између њихових центара једнако:
Ако круг полупречника \(r\) додирује леву ивицу екрана, тада је x координата његовог центра једнака:
На основу овога, допуни наредни програм.
Још један начин да се овај задатак реши је тај да се примети да су координате центара кругова редом \(r\), \(r + 2r\), \(r + 4r\), \(r + 6r\) итд. Дакле, x координата круга са редним бројем \(i\) је \(r + 2\cdot i\cdot r\) тј. \((2i+1)r\). Реши задатак коришћењем ове формуле.
Трећи начин би могао искористити могућност да се функцијом range
може вршити набрајање са кораком (нпр. range(r, r + 10*2*r + 1,
2*r)).
Вертикално распоређени кругови¶
Прикажимо сада како можемо распоредити кругове вертикално.
Напиши програм који црта кругове полупречника 10 пиксела равномерно распоређене вертикално средином екрана, тако да су им центри удаљени 50 пиксела (нацртај све кругове који се виде). Висина екрана се мења приликом сваког покретања програма.
Овај задатак је сличан претходном, уз неколико важних разлика. То што
су кругови распоређени вертикално уместо хоризонтално не мења пуно -
само је потребно заменити улогу x и y координата. Растојање између
полупречника је овај пут фиксно (износи 30 пиксела) и не израчунава се
на основу полупречника. Кључна разлика је то што број кругова није
унапред задат већ је кругове потребно цртати све док се бар неки њихов
делић види на екрану. Зато имамо две могућности. Или ћемо некако на
основу висине екрана израчунати број кругова који се виде или ћемо
уместо бројачке петље for употребити условну петљу while.
Ово друго може бити једноставније.
Правоугаона мрежа¶
Напиши програм који исцртава правоугаону мрежу која се састоји од 100 правоугаоних поља, распоређених у 10 врста и 10 колона (исцртати само линије мреже и то хоризонталне линије плавом бојом, а вертикалне црвеном, дебљине 5 пиксела).
Основни задатак је одредити координате x вертикалних линија и
координате y хоризонталних линија. Ширину једног правоугаоника можемо
одредити дељењем ширине прозора бројем колона (у нашем случају то је
10), док висину једног правоугаоника можемо одредити дељењем висине
прозора бројем врста (то је поново 10). Означимо те димензије са
\(d_x\) и \(d_y\). Вертикалне линије се онда налазе на
растојању \(d_x\), \(2 d_x\), \(3 d_x\), …, \(9
d_x\) пиксела од леве ивице прозора (то су им координате x). Пошто се
те линије простиру од врха до дна прозора, координате y су им једнаке
нули, односно висини прозора. Понављање цртања линија остварујемо,
наравно, употребом петље for, при чему је најбоље да се бројач
i креће од један до девет, јер се тада у кораку i црта линија
од тачке (i*dx, 0) до тачке (i*dx, visina). Цртање
хоризонталних линија остварујемо веома слично, у независној петљи
for у којој се црта линија од тачке (0, i*dy) до тачке
(sirina, i*dy).
Још један начин да се одреди координата наредне линије је да се координата претходне линије увећа за ширину тј. дужину правоугаоника.
Шума¶
Уместо примитивних геометријских облика (кругова, правоугаоника, дужи и слично) можемо распоређивати сложеније облике и тако добити интересантне цртеже.
Нацртај шуму у којој су јелке распоређене једна до друге тако да се центар прве јелке налази на 100 пиксела од леве ивице екрана и да је размак између сваке две суседне јелке једнак 200 пиксела.
Јелку смо већ цртали у неком од претходних задатака. Претпоставићемо
зато да на располагању имамо функцију jelka(x, y) која црта јелку
тако да јој је сидро постављено у тачку (x, y), при чему се сидро
налази на дну стабла, хоризонтално на његовој средини.
Допуни наредни кôд петљом у којој ће се позивати функција за цртање јелке.
Штала¶
Још је лакше ако распоређујемо готове слике учитане из png или
jpg датотека.
У штали живи пет кравица. Напиши програм који их распоређује тако
да стоје једна поред друге, на дну прозора. Слику кравице учитај из
датотеке kravica.png.
Пре него што решиш задатак, подсети се неколико основних функција у вези са сликама.
-
Повежи наредбе са оним чему служе.
Покушај поново!
- slika = pg.image.load("slika.png")
- учитавање слике из датотеке
- slika.get_width()
- очитавање ширине слике
- slika.get_height()
- очитавање висине слике
- prozor.blit(slika, (x, y))
- приказивање слике на екрану
Пре слике са редним бројем i налази се тачно i слика, па се x
координата леве ивице те слике може добити множењем ширине слике са
i. Пошто слика треба да буде на дну прозора, y координату њеног
горњег левог темена можемо израчунати тако што од висине прозора
одузмемо висину слике.
Допуни наредни програм на основу претходне дискусије.

Наравно, могуће је било употребити и петљу наредног облика:
Домаћи задатак - кућице¶
Напиши програм који исцртава низ белих кућица дуж једне улице. Kuћица има квадратну основу и кров у облику једнакостраничног троугла. Врата су постављена на средини основе, висина им је пола висине основе, а ширина четвртина ширине основе.
Дефинисаћемо прво функцију која црта једну кућицу. Цртање ћемо вршити релативно у односу на сидро постављено у доње лево теме кућице и димензију (представљену ширином кућице).
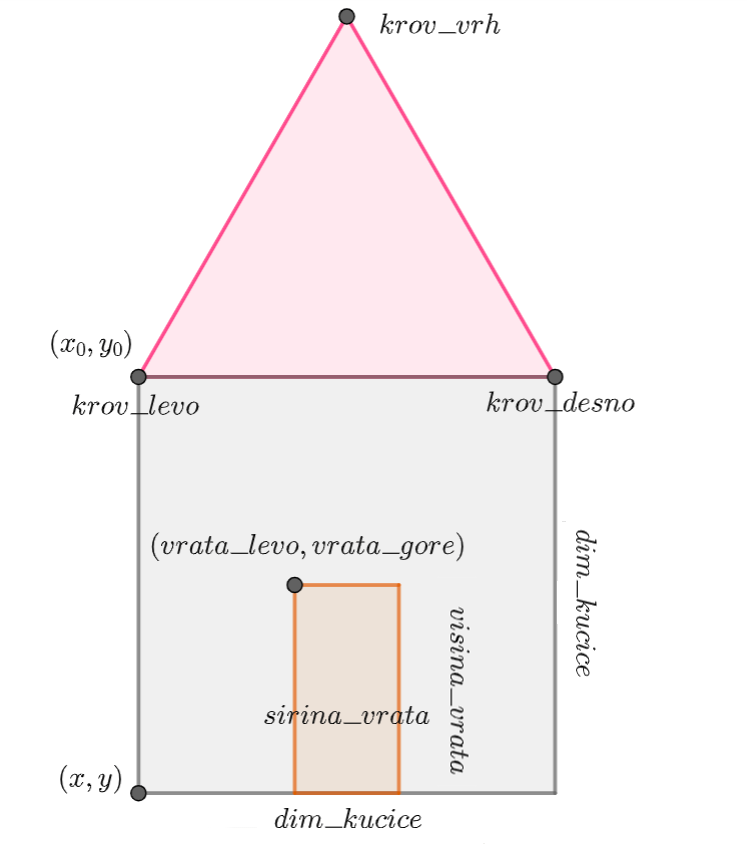
Уз помоћ претходног цртежа израчунај координате свих значајних тачака и допуни програм.

